摘要
深部组织的光学成像长期受光散射的限制.若能在深度超过一个传输平均自由程的组织中,实现光的有效聚焦,就能够显著提升光学成像和光学治疗的效果.
基于时间反转超声编码(TRUE)的波前整形方法利用在生物组织中散射远弱于光的超声焦点作为“导星”,以实现光的聚焦.然而,传统 TRUE 的性能受到超声焦点尺寸和声压标记效率的限制,尤其在声学性质高度非均匀的介质中这一问题更为严重.此外,即便是改进后的迭代 TRUE 方法,由于计算与实验过程耗时较长,也在很大程度上限制了 TRUE 技术的实际应用.
为了解决上述问题,我们提出了一种方法,称为基于时反光声波引导的时间反转超声编码光学聚焦(TRPA-TRUE).该方法将两部分结合起来:一方面利用时间反转的光声(PA)信号,在声学非均匀介质中实现高精度的超声聚焦;另一方面结合光学相位共轭(OPC),利用超声对在散射介质中传播的相干漫射光进行调制,从而实现光在散射介质内部的动态聚焦.
仿真结果表明,与传统 TRUE 相比,该方法的聚焦精度显著提高,更适用于存在严重声学畸变的实际应用场景,例如经颅光聚焦.
这篇文章解决的是复杂介质中,对于一个给定的目标进行光学聚焦的问题.
1. 引言
在生物医学成像研究中,实现深层组织的光学成像仍是一项未解的难题.若能在深部组织中实现光的聚焦,不仅能够增强光学成像系统(如荧光成像)的输出信号强度,还能显著提高成像的灵敏度与成像深度.同时,深层聚焦的光还能直接应用于光遗传学、光动力治疗、激光消融等需要光能量集中作用的领域.
然而,光学成像长期面临的主要挑战之一是组织散射.强烈的散射会在光通过组织时使其波前发生畸变;与此同时,光子在传播过程中还会被组织吸收,从而严重限制光向更深层生物组织的穿透.
当光束进入组织后,光子会发生多次散射,在传播距离达到传输平均自由程(transport mean free path)后,其运动轨迹将变得随机化.
直到最近,大多数用于组织内部成像的光学技术仍主要依赖未发生散射的“弹道光子”(ballistic photons),例如共聚焦显微成像、双光子显微成像以及光学相干层析成像(OCT).
因此,如果能够在散射介质内部实现光的有效聚焦,将有望彻底革新深层组织的无创荧光显微成像、光镊技术、光遗传学、显微手术及光治疗等诸多生物光子学应用领域.
波前整形(wavefront shaping)或许是解决这一问题的最佳途径,其核心思想是通过调节入射光的波前来抵消组织散射带来的影响.目前,主要有三大类波前整形方法正在被积极研究和发展,包括:
- 基于模型的波前整形
- 基于反馈的波前整形
- 光学时间反演/光学相位共轭(optical time reversal/optical phase conjugation,OPC)
基于模型的波前整形依赖数值计算,即利用样本的数字模型进行波前求解.用于计算的输入(样本的显微折射率分布模型)是从成像数据中获取的.
基于反馈的波前整形则依赖于目标位置的强度反馈信号,通过某些先进的优化算法(如遗传算法,甚至深度学习方法)寻找到能使反馈信号最大化的最佳波前.此类反馈信号通常由相机测量散射光获得,但在生物组织内部放置相机并不现实.
Lai 等人提出利用光声信号作为反馈来优化光的波前,使得基于反馈的方法得以适用于生物组织.尽管如此,波前优化过程往往耗时较长,这也限制了其在更广泛领域的应用.
另一种方法是采用光学相位共轭(OPC).在该方法中,只需对来自位于浑浊介质后方或内部光源的散射光子进行一次测量,即可获得最优波前.随后,通过相位共轭镜回放该场的共轭波前,便可以在介质中形成光学焦点.与基于反馈的波前整形类似,OPC 同样需要在散射介质中引入一个“导星”,以对波前聚焦进行引导.
为了解决这一问题,Xu 等人提出了一种称为时间反转超声编码(TRUE)的光学聚焦方案,将超声焦点作为“导星”.
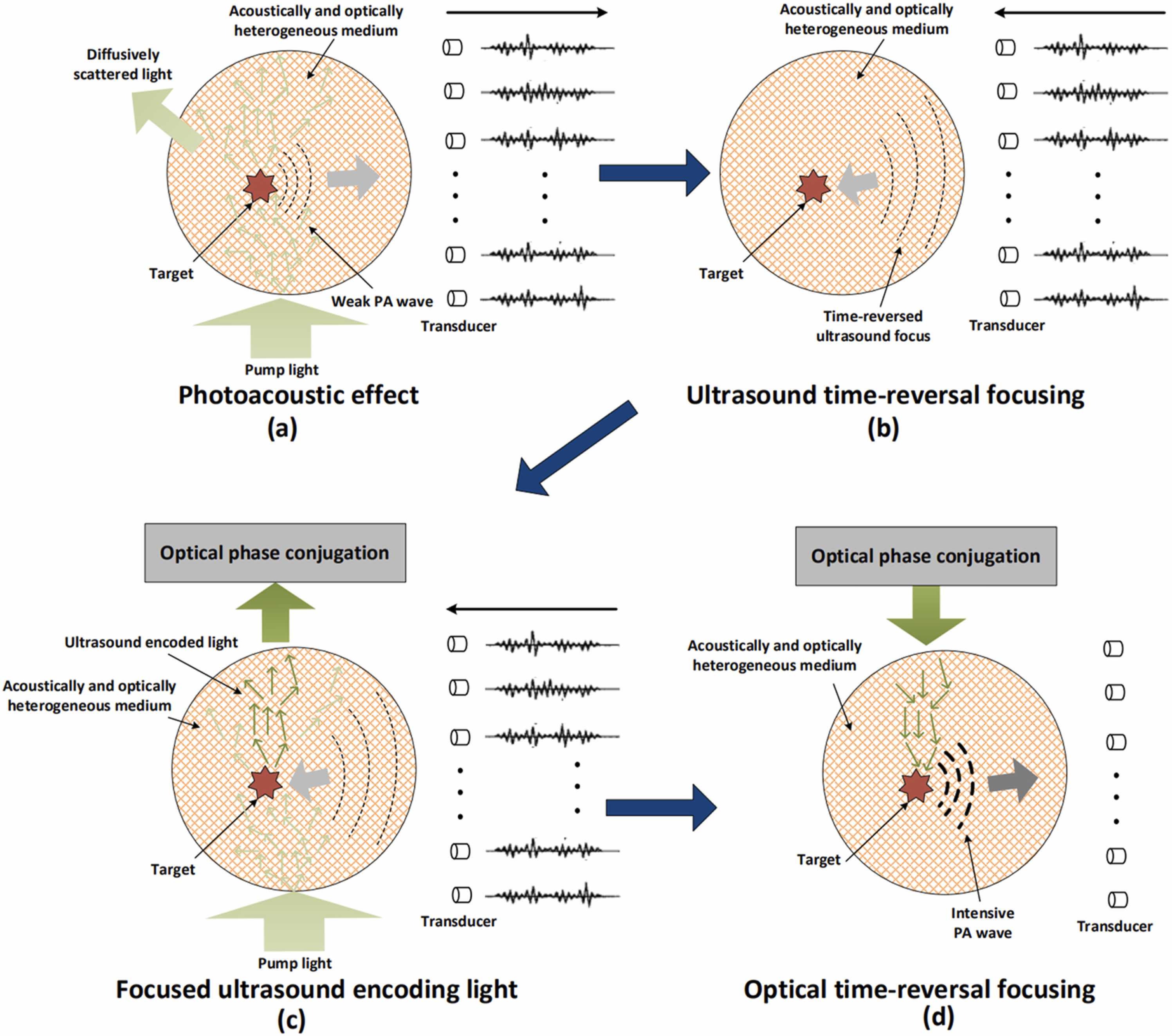
Fig. 1 展示了 TRUE 的工作过程.与光相比,超声在生物组织中的散射要弱得多,因此可以利用声光效应在组织内部产生一个频率发生偏移的虚拟光源,作为“导星”.由聚焦超声换能器发出的聚焦超声会对散射光子进行调制(即超声编码)(Fig. 1a).被编码的光子因而发生频移,在超声聚焦区域形成“导星”.
即声光效应.
作为一个“新的”光源,“导星”与参考光形成干涉条纹,并由全息记录介质记录下来.当全息图被再现时,相位共轭的物光通过时间反转返回至超声调制区域,在散射介质内部形成一个光学焦点(Fig. 1b).

Fig. 1: TRUE 光学聚焦原理的简化示意图.
(a) 起初,一束宽光束或窄光束入射到散射介质中.进入散射介质后,数十亿个光子发生多次散射,其传播路径变得随机.当散射光子经过超声照射区域时,其中一部分光子会被超声“标记”,产生频移.白色实线表示这部分被标记光子的传播路径,它们最终到达 SLM(空间光调制器)并被记录下来.(b) 通过全息方法,我们可以求得被标记光子的相位,并将其相位取共轭后加载到 SLM 上.这样一来,这些光子会沿着原先的路径反向传播,重新汇聚回超声照射区域,就好像“回到了过去”一样.
早期 TRUE 技术的分辨率由超声焦点的尺寸决定(约 25–50 μm).然而,超声的聚焦能力对于保证靶区域内具有足够局域化的能量沉积以及足够数量的光子被调制是至关重要的(见第 2 节 方法).当靶区域位于声学性质高度非均匀的层(如形状不规则的脂肪层或骨组织)之后时,超声的聚焦性能就会成为限制其广泛应用的主要瓶颈.
为了解决 TRUE 分辨率受限的问题,人们提出了一种可能的改进方案——迭代 TRUE.其基本思路是通过共轭场与探测场之间的反馈循环,在实验中实现了将焦点尺寸缩小约三倍的效果.然而,迭代方案耗时较长,会显著增加系统的复杂度.
近期,有研究提出在靶区域产生光声(photoacoustic, PA)信号作为替代方案.例如,Fink 等人已经成功验证了光声信号时间反转的可行性.此外,我们此前的工作也表明,通过对光学选择性靶标在非选择性背景中的经颅光声信号进行时间反转,可以实现对超声聚焦的有效引导.
在本文中,我们提出了一种将光声、超声时间反转以及光学相位共轭(OPC)混合集成的方法,仅依靠一次快照测量,即可在同时具有光学和声学非均匀性的介质中,实现实时超快的二维/三维光学聚焦.
2. 方法
我们提出了一种方法,称为“时间反转光声波引导的时间反转超声编码光聚焦”(time-reversed photoacoustic wave guided time-reversed ultrasonically encoded, TRPA-TRUE).该方法将由时间反转光声(PA)信号引导的超声聚焦,与通过光学相位共轭(OPC)对散射相干光进行的超声调制相结合,从而实现将光动态聚焦到散射介质内部.Fig. 2 展示了该方法的基本原理示意图.

Fig. 2: TRPA-TRUE 的基本流程
(a)首先,将来自激光光源的未聚焦光(λ = 532 nm)注入介质中,光学吸收区域通过光声效应充当声源,产生光声波并被探测器检测.图中给出了 TRPA-TRUE 光学聚焦原理的简化示意图.(b)随后,我们对接收到的 PA 信号进行时间反转操作,从而实现在介质内部的超声聚焦.(c)当时间反转后的 PA 信号到达光吸收区域时,部分光子会在这一快照时刻在光吸收区被“标记”,并随后到达 OPC.(d)最后,我们执行 TRUE 操作以完成整个 TRPA-TRUE 过程.
首先,将来自激光光源的未聚焦光(波长 λ = 532 nm)照射到介质中.具有光学吸收的区域通过光声效应充当声源,产生的光声波由换能器阵列探测(见Fig. 2a).
这里要求组织内必须存在一个足够局域且可产生可测光声信号的吸收体?但假如是完全的均匀材料,或存在多个吸收体,可能都存在问题.
随后,我们对接收到的 PA 信号进行声学时间反转操作,在介质内部实现超声聚焦(Fig. 2b).当时间反转后的 PA 信号到达光学吸收区域时,部分光子将在这一快照时刻在光吸收区域被“标记”,并随后到达 OPC(Fig. 2c).
通过这一步,实现超声信号的精确聚焦,为下一步声光调制做准备.
非常有意思的一点,通过声学时间反转操作,完全不依赖传统声透镜通过结构引入的空间相位延迟,从而直接实现聚焦操作
这里的 guide star 似乎完全取决于组织内光声吸收体的尺寸,从而已经限制了分辨率的上限?
最后,我们执行 TRUE 操作,完成整个 TRPA-TRUE 过程,从而在同时具有光学和声学非均匀性的介质中,仅依靠一次快照即可实现实时超快的二维/三维光学聚焦.
回到 Lihong V. Wang 等人的 Nature Photon (2011)
我们的方法可以直接构建在任意现成的 TRUE 系统之上,这意味着该方案具有“即插即用”的特性.
在接下来的章节中,我们将首先介绍声光效应,并说明为何超声的聚焦位置决定了我们所获得的真实效应.随后,我们将阐述光声信号时间反演的可行性.最后,我们还将通过模拟研究来验证我们的方法.
2.1. 浑浊介质中的声光相互作用
目前,对声光效应的解释主要有三种公认的机制:
- 声场引起浑浊介质中散射体的位置移动;
- 声场产生的机械应变导致介质折射率发生扰动;
- 声场作用下介质发生压缩和稀疏,从而使其光学性质受到扰动.
然而,第三种机制作用极其微弱,因此在此可以忽略不计.
2.1.1. 超声诱导的折射率变化
将位置 $\mathbf{r}$、时刻 $t$ 处的声压场记为:
$$P(\mathbf{r},t)=P_{0}sin(\omega_{a}t-\mathbf{k}_{a}\cdot\mathbf{r}) \tag{1}$$
其中 $P_{0}$ 为声压幅值,$\omega_{a}$ 为声波角频率,$\mathbf{k}_{a}$ 为声波矢量.
声波在介质中传播会产生应变,从而改变介质的局部介电常数.绝热压致光学系数:
$$\eta = \frac{\partial n}{\partial p}$$
把折射率 $n$ 的变化与声压 $P(\mathbf{r},t)$ 联系起来.折射率的变化可表示为:
$$ \Delta n = n_{0}(\frac{\partial n}{\partial p}) P(\mathbf{r},t) \tag{2}$$
其中 $n_{0}$ 为在没有超声调制时的背景折射率.
2.1.2. 超声诱导的散射体位移
为了描述任意粒子的位置,我们用如下方程来对位置 $\mathbf{r}$、时刻 $t$ 处粒子的超声诱导位移建模:
$$ \mathbf{A}(\mathbf{r},t)=A_{0}\ \hat{\mathbf{k_{a}}}\sin(\omega_{a} t-\mathbf{k}_{a}\cdot\mathbf{r}+\Phi) \tag{3}$$
其中,$\mathbf{A_{0}}$ 为位移幅度,$\hat{\mathbf{k_{a}}}$ 为 $\mathbf{k}_{a}$ 的单位矢量,$\Phi$ 为粒子位移与超声压强之间的特定相位差.最近,Huang 等人在散射介质中研究了超声–光相互作用,根据其理论可知
$$\mathbf{A_{0}} = \frac{P_{0}}{\omega_{a}\rho v_{a}}$$
其中 $\rho$ 为背景介质的密度,$v_{a}$ 为声波传播速度.在他们的理论中,当粒子发生运动时,粒子位移与超声压强之间的相位差 $\Phi$ 近似可取为 $ 3\pi /2 $.
由式 (2) 和式 (3) 可以很容易看出,在进行蒙特卡洛(MC)模拟时,无论是由超声诱导折射率变化还是由超声诱导散射体位移所致,超声编码光子的数量都与声场强度呈正相关.
2.1.3. 散射介质中的超声标记效率
另一个需要考虑的重要因素是标记效率.这里用 $\eta$ 表示标记效率,其数学表达式为
$$ \eta = \frac{P_{\mathrm{tag}}}{P_{\mathrm{untag}} + P_{\mathrm{untag}}} \tag{4} $$
其中,$P_{\mathrm{tag}}$ 为被超声压强“标记”的光功率,$P_{\mathrm{untag}} + P_{\mathrm{untag}}$ 为穿过超声压强场的光的总功率.需要注意的是,这里我们只考虑经过超声压强场的那部分光,而不是所有光子的总功率.
由于我们没有推导出标记效率与超声压强场之间的解析表达式,因此在此通过仿真来验证它们之间的关系.
为了计算标记效率,我们只需考虑一个从颅骨射出的散斑的功率谱,并用电场 $E(t)$ 来表示它.设
$$ E(t)=\sum_i E(\theta_i,t)$$
其中 $\theta_{i}$ 表示该散斑中的第 $i$ 个光子.由于在蒙特卡洛(MC)仿真中,各光子相互独立,我们并未将光子视为波动现象,因此忽略了相位和偏振等特征.于是功率谱可以通过下式计算:
$$ \mathbb{E}{|\mathcal{F}[E(t)]|^2} = \mathbb{E}{ \sum_{i} |\mathcal{F}[E(\theta_{i}, t)]|^2 } \tag{5}$$
其中 $\mathbb{E}$ 表示期望运算,功率谱可由 $|\mathcal{F}[E(t)]|^2$ 得到.根据上述定义,我们可以通过所有散斑功率谱的整体平均来估计标记效率.但对所有散斑逐一计算在数值上开销巨大,因此可以仅抽样一部分穿过散射介质的光子来估计标记效率.
多谢 Yujia Huang 在 GitHub 上公开了他们的超声标记代码并上传了实验数据.我们下载并测试了该代码,得到了标记效率与超声压力及超声频率之间的关系.比较结果如 Fig. 3 所示.

Fig. 3: 在 1 MHz、2.25 MHz 和 3.5 MHz 声频条件下,标记效率随声压变化的关系.
图3表明,超声压强越高,超声标记效率越高.这也与我们的预测一致,即超声焦点决定了 TRUE 的真实聚焦能力.
同时,我们还可以看到,随着频率的升高,标记效率逐渐下降.为了获得更小的超声焦斑,我们需要采用更高的超声频率(例如 50 MHz),但这又会导致如图3所示的超声标记效率下降.
此外,高频声波更容易被颅骨衰减和畸变,从而大大降低其穿透深度.相比之下,我们提出的方法利用时间反转的光声波在声散射介质(如颅骨)中精确聚焦超声,从而显著提高标记效率.
综上所述,为了在 TRUE 系统中实现更好的光学聚焦,我们首先需要提高超声标记“导星”的效率,而我们的方法能够在这一性能上获得大幅提升.
2.2. 光声信号的时间不变性
光学吸收区域通过光声效应可以作为声源,其过程可由下式描述:
$$ \Delta p - \frac{1}{c^{2}}\frac{\partial^{2} p}{\partial t^{2}} = -\ \frac{\beta}{c_{p}}\ \frac{\partial H}{\partial t} \tag{6} $$
其中, $p(r,t)$ 为位置 $r$、时刻 $t$ 处的声压, $c$ 为声速, $\beta$ 为等压热膨胀系数, $c_p$ 为比热容, $H$ 为单位时间内单位体积的光能量密度.
若 $p(r,t)$ 是该方程的一个解,则 $p(r,−t)$ 也是其解.换言之,该方程在时间反演下保持不变.因此,从某一声源向外发散传播的波可以在时间上反转,并在空间中反向传播而重新汇聚到该声源处.
3. 在脑模型上模拟 TRPA-TRUE
我们的方法通过在混浊介质中、基于脑模型(Fig. 4a)进行 TRPA-TRUE 模拟来验证,该脑模型下载自 Scalable Brain Atlas.

Fig. 4: 模拟环境建模过程示意图.
(a) 从 MRI 数据中获取每一层切片.(b) 将脑部 MRI 数据导入 MATLAB,并通过阈值分割将其分为空气、水、中脑、白质、灰质、脑脊液、头皮和颅骨.(c) 在对每层切片完成分割后,将处理后的 MRI 图像叠加构建三维模型,并将其加载到 k-Wave 模拟工具中.
声学模拟在 k 空间中实现,使用 MATLAB(R2019a,MathWorks Inc., Natick, MA, USA)的 k-Wave 工具箱,其能够提供原始 PA 数据,并模拟时反声波的传播过程.
在光学模拟部分,我们采用了蒙特卡洛(MC)光子传播模型.该模型已被广泛应用于声光成像(AOI)模拟,因为它能够直接模拟声光在介质中的相互作用.
模拟介质的参数可通过掩膜操作,根据脑模型分配相应的数值来设定.不同颅内传播介质的属性列于表 1 中.
| Tissue | Speed [m/s] | Density (Kg/) | Absorption [dB/ (MHz)] | Img-pixel -values |
|---|---|---|---|---|
| air | 343 | 1.2 | 0.0004 | [0] |
| water | 1475 | 1000 | 0.05 | [0] |
| midbrain | 1546.3 | 1000 | 0.6 | [21–39],[51–78] |
| white matter | 1552.5 | 1050 | 0.6 | [40–50] |
| gray matter | 1500 | 1100 | 0.6 | [81–220] |
| spinal fluid | 1475 | 1000 | 0.05 | [1–9] |
| scalp | 1540 | 1000 | 0.1 | [10–20] |
| skull | 3476 | 1979 | 2.7 | [221–255] |
表1 | 基于图像像素值在模型中分配的声速、密度和吸收系数.
如 Fig. 4 所示,将脑部 MRI 数据导入 MATLAB,通过阈值分割将其划分为空气、水、中脑、白质、灰质、脑脊液、头皮和颅骨等组织.由于在本实验条件下 MRI 图像的分辨率已足够高,因此我们直接依据图像像素值对每一层切片进行分割,其结果见表 1 的第四列.
完成各层切片的分割后,将处理后的 MRI 图像沿切片方向堆叠,形成三维模型,再将该模型导入 k-wave 仿真包中.Fig. 4 展示了整个分割流程以及声学脑仿真配置过程的各个步骤.
本实验需要使用相控阵超声发射与探测系统.我们预期,采用更多的超声阵元以及具有更大角度覆盖范围的环形或弧形探头,将有望获得更好的光学聚焦效果.为更好地模拟实际应用场景,此处设置了一个 64 通道线阵探头.
Fig. 4c 所示的仿真配置中,在 xz 平面中心周围布置了 64 个换能器,用于获取样品产生的光声(PA)信号.中心到各声学传感器的距离为 $40 mm$.传感器被设定为具有无限带宽的理想超声探测器.仿真中颅骨外介质的声速设定为 $1500 m/s$,这些传感器以 $150 MHz$ 的采样频率记录整个介质中的光声声压.
4. 结果
4.1. 失真介质中基于 TRPA 的聚焦
由于光速远大于声速,当光通过超声场时,可以认为超声场在该过程中近似静止.因此,这里我们采用 ROI 内各点记录到的最大声压值来评估声学聚焦能力.
PA 信号由 MATLAB 中的 k-Wave 仿真产生,经颅骨传输后由 64 个声学传感器接收.我们分别获得了采用和不采用时间反转(TR)时声波在初始位置处的聚焦结果.
在 ROI 中心放置了一个尺寸为 $2 mm$、吸收系数为 $5 cm^{-1}$ 的吸收体,用以产生 PA 信号.实验结果如 Fig. 5 所示.我们的仿真环境为三维配置.为了更直观地观察空间中的声学聚焦情况,我们截取了 xy、xz 和 xz 三个不同平面进行对比.Fig. 5 中的红色虚线圆表示吸收体的目标位置.
在使用常规聚焦换能器时,得到的超声聚焦结果如 Fig. 5a 所示.可以看到超声在目标位置实现了聚焦,但在圆盘外部存在大量“热点”,其声压增益与焦点内部相近甚至更高.圆盘边缘向周围组织延伸的局部“热点”可能产生不期望的“导星”,从而影响标记的准确性.
相比之下,采用 TRPA 引导聚焦(Fig. 5b)时,超声在目标位置实现聚焦的同时,圆盘外部的“热点”明显减少.

Fig. 5: 在 xy、xz 和 yz 横截面平面上的模拟声压增益分布.黑色轮廓表示颅骨的形状.
(a) 超声直接聚焦.(b) TRPA 引导聚焦.
4.2. 失真介质中基于 TRPA-TRUE 的光学聚焦
Fig. 6a 给出了在未进行波前整形条件下获取的三维数据堆栈的平均强度投影.为了更直观地观察空间中的光学聚焦情况,我们沿 y 轴截取了三个不同的截面.从Fig. 6a 可以清楚地看到,随着与散射层距离的增加,光通量强度迅速衰减.

Fig. 6: 沿 z 轴方向计算得到的平均强度通量图的仿真结果.
(a) 未进行波前整形.(b) TRUE.(c) TRAP-TRUE.
Fig. 6b 显示的是采用传统 TRUE 方法得到的波前整形后,其光能量通量图像的平均强度投影.可以明显看出,相较于未进行波前整形的情况,TRUE 显著提升了光的聚焦效果.
然而,在 z 轴中部附近(即超声“导星”所在的位置),光焦点略显模糊,焦斑尺寸被拉宽,并且在其上方还出现了一个多余的非期望焦点.更为严重的是,最高强度出现在组织表面附近,而不是预期的焦点处.同时,由于信噪比较低,在这些深度位置上光强不再呈单调变化.
Fig. 6c 给出了采用 TRPA-TRUE 方法得到的波前整形后光能量通量图像的平均强度投影.我们使用时间反转的 PA 信号作为超声调制的激励,用来标记正在传播的光子.
与传统 TRUE 方法相比,该方法得到的通量热图在目标位置呈现出更小的焦斑面积以及更高的强度投影.
5. 讨论与结论
在本工作中,我们首次将光声成像、超声时间反转以及光学相位共轭(OPC)相集成,提出并实验验证了 TRPA-TRUE 方法,实现了在光学与声学均非均匀介质中以单次快照完成的超高速二维/三维光学聚焦.
借助蒙特卡洛(MC)仿真和 k-Wave 工具箱,我们在数值脑模型中证明了该方法能够在更高信噪比(SNR)条件下提升焦点强度,而这在此前的任何 TRUE 系统中尚未有报道.
然而,在实际应用层面,仍然存在许多工程与技术问题亟待进一步考虑和解决.例如,时间反转光声波产生系统与 TRUE 系统之间的信号同步问题,以及多源目标选择问题.如果样品中存在多个吸收体,时间反转光声波将会同时在多个目标区域形成聚焦,因此未来需要设计专门的算法,以实现对特定目标源的选择性聚焦.
除此之外,理论上增加超声探头的通道数有望进一步提升聚焦性能;相应地,如果超声探头的数量减少,系统性能则会受到削弱.在这种情况下,仍可考虑通过设计新的算法来对时间反转光声波进行优化控制,从而部分弥补硬件上的不足.
此外,尽管本研究中时间反转光声信号已证明可以为声光相互作用提供可行的超声聚焦手段,但在活体人脑应用中,颅骨的存在会导致强烈的光散射和衰减,从而使得产生颅内光声信号变得极具挑战性,这一问题目前仍是有待解决的开放性课题.
6. 文章之外的思考
TRPA-TRUE 能否实现任意位置光聚焦?
就这篇文章给出的 TRPA-TRUE 实现而言,最后形成的光焦点,确实只能落在“原始光声源”(即最初产生 PA 信号的吸收体)的位置上,而且如果有多个光声源,还会在多个源点上同时成光焦点.
链条:未聚焦光线 → 原始光声源 → 产生 PA → 时间反转 → 在原始光声源处形成超声焦点 → TRUE → 在该超声焦点处形成光焦点
换句话说,该文章提出的方法下,光确实只能聚焦到那些一开始就存在、并且产生了 PA 的吸收体位置上,并不能实现任意指定位置的光聚焦.
时间反转本身只会聚焦到“原始光声源”的位置,能否在附近其他位置成像/聚焦?
在原始光声源附近微调焦点是有可能的.参考文章 Time reversal of photoacoustic waves,为了在附近其他位置成像/聚焦,作者在时间反转信号上再叠加线性延时法则,相当于在“已校正相位”的基础上再做常规波束转向.
实验表明,在一定范围内(几倍焦斑宽度),焦点移动后仍保持良好的聚焦质量.
这种聚焦位置的限制,应用场景是否非常受限?
在实际场景里,依然有很多可能的应用点:
很多场景中只关心光的强吸收区域
靶向递送造影剂至目标区域,可以调控希望聚焦的区域
对于很多“靶向治疗/刺激”类任务,锁死在 ROI 反而是优势,如深部肿瘤光热/光动力疗法,经颅光刺激/光遗传