摘要
本工作提出并实现了一种新型的高自由度开环自适应光学方法——数字光学相位共轭(digital optical phase conjugation, DOPC),用于构建一种稳定可靠的光电一体化光学相位共轭系统.
我们证明,该原型系统在约 3° 的角度范围内,相位共轭精度可达约 $3.9 × 10^{-30}$,并且能够实现入射光场穿过相对较厚的浑浊介质($μₛl ≈ 13$)的相位共轭重建.
进一步地,我们利用该系统研究了在浑浊介质中,利用相位共轭逆转随机散射的鲁棒性,结果表明这种逆散射过程对相位误差具有出乎意料的容忍度.即使 OPC 波前存在显著的空间相位误差(误差在 –π/2 到 π/2 区间内均匀分布),其在散射介质后实现的相位共轭重建效率仍可达到无相位误差理想 OPC 情况下的约 40%.
1. 引言
一般来说,在光学波段内,生物组织可以看作高度浑浊的介质.组织对光的强烈散射,是限制深层组织光学成像和光学传感的重要因素之一.近些年,多篇工作已经实验证明,通过对入射光场的波前进行恰当调制,可以在一定程度上削弱散射带来的影响.
例如,Mosk 课题组利用空间光调制器,对入射光场的波前进行调节和优化,从而实现了通过散射介质的聚焦.我们课题组则证明,对样品一次透射所得光场进行光学相位共轭(optical phase conjugation, OPC)复制,同样可以逆转这一次散射造成的影响.
利用光学相位共轭来抑制组织浑浊具有很大吸引力,因为它只需要对透射光场进行复制,并将波前上各点的相位取相反数即可.光学相位共轭自 20 世纪 70 年代以来一直是一个活跃的研究方向,已经发展出许多应用,例如新型谐振腔结构、高分辨率图像投影以及光学计算器件等.
传统上,OPC 波的产生依赖各种光学非线性效应,例如光折变效应和布里渊散射.基于非线性光–物质相互作用的 OPC 技术在原理上可以处理大量的光学自由度;然而,这类技术通常只能提供有限的相位共轭反射率(即相位共轭信号功率与输入信号功率之比).此外,它们往往需要专用的光源和特定的非线性介质.从实用的角度来看,如果能够构建一种 OPC 系统,可以兼容不同波长、不同相干长度以及不同功率水平的光源,将更加理想.
另一类前景广阔的光学方法是自适应光学.自适应光学利用波前传感器和波前调制器来测量并补偿相位像差.自适应光学技术最初是为补偿天文望远镜中的大气扰动而发展起来的.在过去二十年中,已有多个研究团队将自适应光学技术应用于光学显微成像,用于补偿显微成像系统本身的像差,以及样品内部折射率变化所引入的像差.在这些应用中,像差的量级通常相对有限,并且往往可以分解为若干阶 Zernike 多项式来描述.在这种情况下,常采用可变形反射镜作为波前调制器,以提供足够的像差补偿能力.
最近,Mosk 团队利用高通量的空间光调制器,实现了逐像素优化的控制方法,在高度浑浊的样品($μₛl ≈ 10$,其中 $μₛ$ 为散射系数,$l$ 为样品厚度)中成功形成了光学焦点.
在本工作中,我们提出了一种高容量(约 10⁶ 个自由度)的开环自适应光学方法——数字光学相位共轭(digital optical phase conjugation, DOPC),用于在浑浊介质($μₛl ≈ 13$)中实现快速相位共轭.与基于非线性光学的 OPC 系统相比,DOPC 具有两个显著优势.首先,作为一种自适应光学方法,所产生的 OPC 波的功率与输入信号无关,可以在较宽范围内自由调节.其次,同一套 DOPC 系统在原理上既可适用于连续波激光,也可用于脉冲激光,并能覆盖不同功率水平.这两点对于生物医学应用尤为重要.
此外,DOPC 所能控制的光学自由度远高于传统自适应光学方法,因此能够在高度浑浊样品中实现相位共轭.又由于 DOPC 是对整个波前进行并行处理,本质上是一种快速的波前优化过程,因此具有用于体内生物医学应用的潜在可行性.
由于在 DOPC 系统中波前是通过数字方式控制的,我们还可以利用该系统来研究随机散射介质中相位共轭的基本性质.DOPC 系统尤其适合用来探讨这样一个具体问题:当相位共轭波前中存在相位误差时,通过随机散射介质实现的光学相位共轭(OPC)对这些误差究竟具有多大的容忍度.借助 DOPC,我们可以以高度可控的方式在波前中人为引入相位误差.
利用我们的原型系统,我们在实验中发现,一个有悖直觉的现象是:即使存在相当显著的相位误差,通过随机散射介质实现的 OPC 依然表现出出乎意料的鲁棒性.我们的实验结果与基于传输矩阵形式主义得到的理论预言符合良好.
2. 设计
要以数字方式生成相位共轭波,我们只需要一种既能作为传感器、又能作为执行器的器件.用于声学时间反转实验的压电换能器就是一个很好例子.可惜的是,在光学处理领域,目前还没有这样一种器件.
我们可以通过将波前测量装置(传感器)与空间光调制器(SLM,执行器)组合,并按照 Fig. 1 所示方式进行光学布置,来实现一个等效系统.如果这两个部件彼此精确对准,使得每个器件都在另一个器件平面上形成虚像,那么这个复合系统就能够正常工作.
换句话说,我们希望传感器的每一个像素在执行器上都有一个对应的虚像像素,反之亦然.由于这一方法本质上是一种光电混合实现方案,我们将其称为数字光学相位共轭(digital optical phase conjugation, DOPC).

Fig. 1: DOPC 系统构成
DOPC 系统由两部分构成:波前测量装置(传感器)和空间光调制器(执行器),二者通过分束器在光路中组合在一起,作为一个整体系统,既可以测量输入波前,又可以产生相位共轭的输出波前.(a) 示意波前测量过程,此时参考光与输入信号发生干涉,它们之间的相对相位由电光相位调制器控制;(b) 示意相位整形过程,此时 SLM 对入射的参考光进行调制.
Fig. 1 展示了 DOPC 系统的结构设计,其中使用一个 50:50 分束器,在 CCD 相机和 SLM 之间建立虚像对应关系.OPC 波的产生分为两个步骤.
第 1 步,分束器将输入信号引导到 CCD 相机.一束具有平坦波前的参考光与未知的输入光发生干涉,在 CCD 上形成全息图.输入光与参考光之间的相对相位由电光(EO)调制器控制.通过相移全息技术,我们可以唯一确定输入波的相位和振幅信息.
第 2 步,将测得的波前在计算机中作数字反转,并加载到 SLM 上.参考光照射到 SLM 后,其反射光被调制,并沿与原始输入光相反的方向传播,从而形成输入信号的相位共轭波.
DOPC 系统具有以下优点:
同一套系统既可用于连续波(CW)激光,也可用于脉冲激光;
DOPC 系统在工作波长和光强上都具有很高的灵活性,基本不受限制;
产生的 OPC 波的功率与输入信号无关,并且可以通过计算机精确控制,因此可以任意调节 OPC 反射率(定义为 OPC 信号功率与输入信号功率之比);
DOPC 系统的工作方式是开环的,不需要任何迭代式的测量或计算;
数字控制的自由度数量巨大,使我们可以灵活地改变 OPC 的波前.
其中,第 5 点的特性在研究 OPC 波与浑浊介质之间的相互作用时尤为重要.
3. 实现
本节将讨论 DOPC 系统在实验中的具体实现方法,以及所需的标定步骤.标定的目的在于保证“实测波前”与 SLM 输出之间建立起精确的一一对应关系.
3.1 实验装置
Fig. 2 给出了 DOPC 系统的实验装置示意图.实验中使用了一台波长为 532 nm 的固体连续波(CW)激光器(Spectra-Physics, Excelsior Scientific 200 mW).激光输出先通过半波片,再由一个非偏振分束器(BS1)分成两束.
其中一束经过电光相位调制器(EO phase modulator)后进入待处理的应用系统.另一束则经过空间滤波,作为 DOPC 系统的参考光束使用.参考光先被偏振分束器(PBS)引导,再射向布置在 SLM(768 × 1024 像素)前方的非偏振分束器(BS2).
理想情况下,BS2 应放置在 SLM 与 CCD 之间的对称平面上,使得 SLM 能在 CCD 上形成镜面对称的像,反之亦然.实际中,由于 CCD 像素尺寸小于 SLM 像素尺寸,我们使用透镜在对称位置成像,得到一个放大的 CCD 像面,如 Fig. 2 中所示的 “CCD 虚像平面”.SLM 安装在一套带有倾斜与旋转调节功能的平台上,由两个差动千分尺(Newport, DM-13)驱动调节.

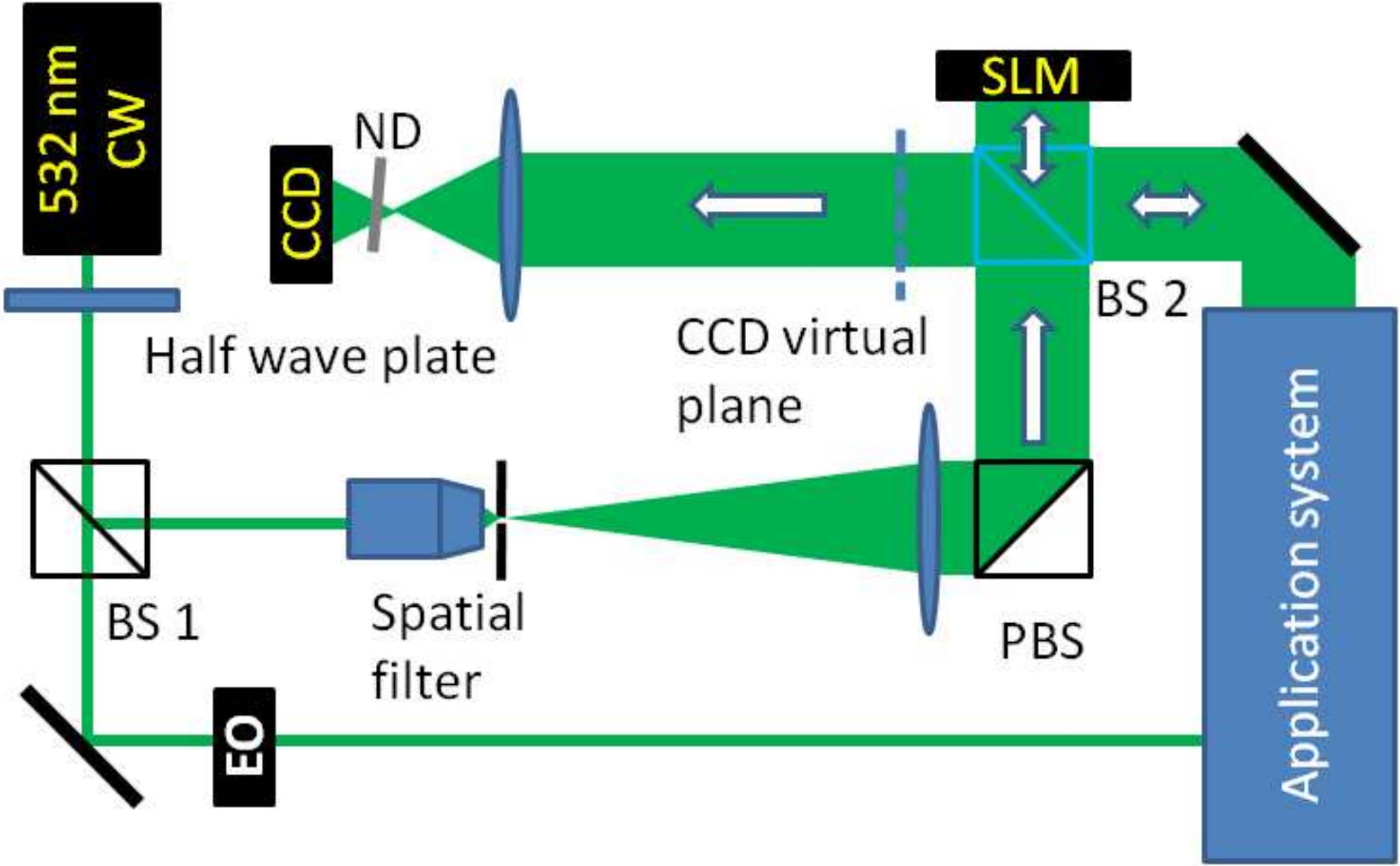
Fig. 2: DOPC 系统的实验装置示意图
激光器为波长 532 nm 的固体连续波激光器(Spectra-Physics, Excelsior Scientific 200 mW).SLM:LCOS 反射式空间光调制器(Holoeye, LC-R 2500);CCD:CCD 相机(ImagingSource DFK41BF02);PBS:偏振分束器;BS1 和 BS2:非偏振分束器;ND:中性密度滤光片.
输入信号从 BS2 的右侧进入 DOPC 系统,与参考光束在 CCD 上发生干涉并形成全息图.信号光束与参考光束之间的相对相位由电光(EO)调制器调制.在相移全息过程结束后,计算机从全息图中提取相位信息,并将其发送给 SLM,使其输出相位共轭信号——这种波相对于输入信号反向传播,且具有与输入信号相反的空间相位分布.相位共轭波的功率由参考光束的功率决定,与输入信号无关,因此我们可以任意控制相位共轭反射率.
需要注意的是,输入波也会进入 SLM,其反射光构成输出波的一部分.设输入信号为:
$$ E(x,y)e^{i\phi(x,y)} $$
当在 SLM 上加载反向相位分布 $−ϕ(x,y)$ 时,经 SLM 反射的输入信号变为:
$$ E(x,y)e^{iϕ(x,y)−iϕ(x,y)}=E(x,y) $$
即得到一束空间相位平坦的波,就像参考波一样.实验中,这部分信号远弱于经 DOPC 正确整形后的输出.
在波前测量过程中,参考光束的一部分会被 SLM 反射并进入应用系统.只要应用系统本身的反射率不太高,这部分反射对波前测量的影响就不大,因为它没有经过 EO 调制器的相位调制.相位整形过程中,参考光束的一部分被引向 CCD 探测器.我们将 CCD 前的 ND 滤光片略微倾斜放置,使其反射光不会重新进入 BS2.
3.2 标定
要使 DOPC 系统正常工作,CCD 与 SLM 必须在空间上正确对应,并且 CCD 测得的相位要被准确地映射到 SLM 上.由于在 DOPC 的设计中,SLM 的反射光场实际上并不会真正落在 CCD 上,因此两者的对准并不能像普通系统那样直接完成.为此,我们设计了一套对准流程:在调节时使用一个类似筛孔结构的掩模作为参考标尺.下面将具体介绍这一流程.
首先需要保证 SLM 与入射的参考光束垂直.为对准 SLM,我们测量了沿原路通过空间滤波器和 Fig. 2 中 BS1 反向传播的光,并通过精细调节带倾斜与旋转调节的平台,使反向传播信号达到最大值,从而完成对准.
更棘手的标定步骤是:要把 CCD 上测得的波前,正确映射到 SLM 的输出上.为此,我们设计了一个三步标定流程,并制作了一块铬膜掩模,其孔径为 10 微米,孔间距为 20 微米.
在第一步中,我们将该掩模放置在 SLM 的对称平面位置,如 Fig. 3(a) 所示.反射式掩模与 SLM 构成了一个迈克耳孙干涉仪.我们先将 SLM 的相位设为 0,然后观察由 SLM 与掩模形成的干涉图样,同时微调掩模的姿态,使其与对称平面平行.掩模安装在一维平移台上.通过测量 SLM 和掩模到分束器的距离,并将两者差值控制在 0.5 mm 以内,可以保证位置精度.考虑到 SLM 像素尺寸约为 20 微米,而波长为 532 nm、束腰半径为 10 微米的高斯光束,其瑞利长度大于 1 mm,因此将距离差控制在 0.5 mm 以内对于标定来说已经足够精确.
我们首先用光照射掩模,并将透射光成像到 CCD1 上;CCD1 也是在实际 DOPC 实验中使用的那台 CCD 相机.
第二步,如 Fig. 3(b) 所示,我们照射 SLM,并将 SLM 成像到另一台相机(CCD2)上.我们把 SLM 划分为 64 × 48 个小块,每块包含 16 × 16 个像素,并将相邻块之间的相位差设为 π.如此陡峭的相位突变会产生散射.如果这些散射光没有被成像系统完全收集,块与块之间的边界在图像中就会显得较暗,我们的实验中确实观察到了这种现象.通过这种方式,我们利用相位调制在 SLM 的成像上产生了一个强度分布图样. Fig. 3(d) 给出了实验获得的 SLM 图像.
第三步,如 Fig. 3(c) 所示,我们再次照射掩模,并将透射光成像到 CCD2 上. Fig. 3(e) 是在第三步中得到的掩模图像.通过比较第二步和第三步获得的两幅图像,我们就可以确定 SLM 像素与掩模上各孔之间的相对位置关系.而第一步得到的图像则告诉我们这些孔在 CCD1 上对应的位置——CCD1 正是实际 DOPC 实验中使用的相机.借此,我们就能够把 SLM 像素精确映射到 CCD1 上.

Fig. 3: CCD 与 SLM 之间映射关系的建立流程
(a)在 SLM 的对称平面处放置掩模,对掩模进行照明,并在 CCD1 上成像.(b)在 SLM 上显示相位图案,并在 CCD2 上成像.(c)照明掩模,并在 CCD2 上成像.(d)实验测得的 SLM 图像.(e)实验测得的掩模图像.
4. 实验测试
接下来,我们通过考察 DOPC 系统对点光源发出光场的测量精度,以及其生成能在该点光源位置重新聚焦的相位共轭光场的能力,对系统性能进行了评估.
4.1 实验装置
实验装置如 Fig. 4 所示.为了得到位置可控的点光源,我们将经空间滤波的光束通过一只数值孔径 NA=1.3 的油浸物镜(物镜 1).物镜 1 安装在由差动千分尺驱动的平移台上(Newport, DM-13),从而可以精确调节其位置.聚焦后的光束由另一只相同的物镜(物镜 2)收集,并引入 DOPC 系统.DOPC 系统产生的相位共轭光束经物镜 2 反向传播,重新聚焦回原来的点光源位置.
为了测量 DOPC 所产生焦点的位置精度和稳定性,我们在物镜 1 后光阑附近放置分束器,将透射的相位共轭光束引向一只透镜,并将其聚焦在 CCD 探测器上.
在第一组实验中,我们沿横向移动物镜 1,如 Fig. 5(a) 所示.此时,从物镜 2 出射的光束会偏离其原本的传播方向. 在第二组实验中,我们沿轴向移动物镜 1,如 Fig. 5(b) 所示.此时,从物镜 2 出射的光束会变成发散或会聚光束.

Fig. 4: 用于测试 DOPC 精度的实验装置示意图
激光器为波长 532 nm 的连续波固体激光器.SLM:LCOS 反射式空间光调制器(Holoeye, LC-R 2500);CCD:CCD 相机(ImagingSource, DFK41BF02);PBS:偏振分束器;BS:非偏振分束器;EO:电光相位调制器(Thorlabs, EO-PM-NR-C4);Lens 1 和 Lens 2:物镜(Olympus, UPLFLN 100XO2,NA 1.3);ND:中性密度滤光片.

Fig. 5: 用于评估 DOPC 补偿范围的透镜 1 位移示意图
(a) 将物镜 1 沿横向移动,此时从物镜 2 出射的光束偏离原来的传播方向.(b) 将物镜 1 沿轴向移动,此时入射到 DOPC 系统的光束变成会聚光或发散光.
4.2 实验结果
实验结果汇总如 Fig. 6 所示.Fig. 6(a) 和 6(b) 分别给出了当物镜 1 相对于中心位置横向位移 50 微米 (a) 和轴向位移 50 微米 (b) 时,通过相移全息测得的波前.
物镜 1 的横向位移使进入 DOPC 系统的光束在 SLM 上的入射角偏离法线方向,因此测得的相位在横向上呈现近似恒定的线性斜坡.对 Fig. 6(a) 进行傅里叶分析可知,相位每经历一个 2π 周期大约跨越 2.5 个像素.
轴向位移则使进入 DOPC 系统的光束变成会聚光或发散光,相应地,相位斜率从中心向边缘逐渐增大.Fig. 6(c) 显示了当物镜 1 在 −60 至 60 微米范围内移动时,重建焦点的位置变化.在 −50 至 50 微米范围内,焦点相对中心位置的标准差约为 0.12 微米,明显小于 0.23 微米的焦斑直径.结合实验中使用的 100× 物镜(焦距 1.8 mm),我们在约 3.2° 的相位共轭范围内,实现了约 3.9×10^-3° 的角度精度.
Fig. 6(d) 给出了当物镜 1 在轴向从 −100 微米移动到 100 微米时,重建焦斑尺寸的变化情况.可以看到,焦斑尺寸的变化是不对称的.
当轴向位移为负时,从物镜 2 出射的光束为发散光,能够照亮整个 SLM.此时,靠近光束中心的相位变化较缓,DOPC 系统可以较为精确地进行空间采样与补偿;而靠近 SLM 外侧区域的相位变化可能超过 DOPC 系统的空间采样能力,从而引入误差.
当轴向位移为正时,从物镜 2 出射的光束为会聚光,只能照亮 SLM 的中心区域.物镜截断了光束中的高空间频率分量,这种截断效应正是 Fig. 6(d) 中出现不对称性的原因.
作为对比,我们在 Fig. 4 的实验装置中用一面平面反射镜替代 DOPC 系统,重新进行了横向和平移轴向位移实验. Fig. 6(e) 给出了横向位移的测量结果,线性拟合得到的斜率为 1.99,这与镜面反射会使角度偏转加倍的预期结果一致. Fig. 6(f) 为轴向位移的结果:在没有 DOPC 补偿的情况下,仅 1 微米的位移就会使反射焦斑尺寸增加到原来的 10 倍以上,达到约 3 微米.

Fig. 6: DOPC 系统在透镜位移下的聚焦补偿性能
(a) 当物镜 1 相对于中心位置横向位移 50 微米时,通过相移全息测得的波前.(b) 当物镜 1 相对于中心位置轴向位移 50 微米时测得的波前.(c) 物镜 1 横向移动时,DOPC 重建焦点的位置变化.(d) 物镜 1 轴向移动时,DOPC 重建焦斑直径的变化.(e) 用反射镜替代 DOPC 后,物镜 1 横向移动时测得的反射焦点位置变化.(f) 物镜 1 轴向移动时测得的反射焦斑尺寸变化.
4.3 DOPC 系统的补偿范围
DOPC 系统的光学自由度受 SLM 和 CCD 相机的像素数限制.在给定像素数的条件下,可以估算 DOPC 系统可补偿的最大横向位移.实验中使用的 SLM 具有 768 × 1024 个像素,这些像素被成像到 CCD 相机上的一块区域,对应的 CCD 像素数略多一些.实际实验时,有 634 × 634 个 SLM 像素被成像到 100× 物镜后光阑上(后光阑直径约为 5 mm).
在奈奎斯特频率下,相邻像素间的最大相位差为 π,因此在 634 个像素范围内的总相位变化量为 634π,对应 317 个波长(317λ).由此可得系统能够补偿的最大角度偏差约为 317λ / 5 mm;而在物镜焦平面上,对应的最大横向偏移为 317λf / 5 mm,其中 f 为物镜的焦距.对于本实验使用的 Olympus 100× 物镜,焦距约为 1.8 mm,在波长 λ = 532 nm 时,理论上焦点相对中心的最大偏移量约为 61 微米.实验中,我们在本系统中实际实现的横向补偿范围约为 50 微米.
5. 使用随机散射介质的评估
DOPC 的一个潜在应用,是在高度浑浊的散射介质中重建给定的光学模式.为验证这一能力,并对我们的方法进行严格检验,我们将 DOPC 系统用于在散射介质中返回一束光学相位共轭(OPC)波,该介质满足 μ_s l ≈ 13.
5.1 实验
我们仍采用 Fig. 4 所示的实验装置进行演示.为了制备随机散射样品,首先将不同直径(0.2、0.5、1、3、5、10 μm)的聚苯乙烯微球按相同质量百分比混合,配制成水溶悬浮液,然后滴加在盖玻片上并干燥.随后在微球上方滴加浸没油,再用另一片盖玻片覆盖,形成散射样品.
参数 μ_s l 的大小可以通过测量透射的弹道光来确定.实验中,我们用直径 1 mm 的准直激光束照明样品,将透射光引入一个直径同为 1 mm、放置在距离样品 3 m 处的光阑(光阑孔径),并用功率计(Newport 1830)测量透射功率.为避免折射导致对 μ_s l 的高估,我们在光路中加入一面反射镜,略微调整透射光的传播方向,确保其中的弹道光分量能够顺利通过光阑.根据弹道光测量结果,我们得到 μ_s l ≈ 13.
散射样品安装在一维平移台上,并插入两只物镜之间.整个实验分三步进行:
第一步:测量光束依次通过物镜 1、散射样品和物镜 2 后的波前.
第二步:在 SLM 上加载相应的相位分布,启动 DOPC 系统.此时,DOPC 输出光应沿着原先在样品中的散射路径“逆行”返回,并在出射后恢复为近似准直光束.
第三步:将 SLM 相位全部设为 0(不进行相位调制),即关闭 DOPC 功能,测量此时 DOPC 输出光通过样品后的透射情况.由于入射到物镜 2 的光束近似为平面波,我们预期在屏上看到的是一幅随机散斑(散射图案).

Fig. 7: DOPC 在强散射介质中光场重建效果
(a) DOPC 测得的相位分布.(b)DOPC 重建的信号.视场约为 12 μm.(c)对照实验:将 SLM 的相位全部设为 0
6. 相位误差对随机散射介质中 OPC 过程的影响
可以合理地预期:在随机散射介质中利用光学相位共轭(OPC)来重建初始入射场,其效果会取决于所产生的共轭相位场有多精确.共轭场的“保真度”与重建效率之间的定量关系非常重要,因为它能够为基于 OPC 的各种应用提供设计参考和优化依据.
然而,使用传统 OPC 方法很难在实验上系统研究这种关系,因为几乎无法在保持其他条件不变的情况下,可控地向共轭相位场中引入特定误差.相比之下,数字光学相位共轭(DOPC)系统则为我们提供了一种简单且高度可控的方式:可以在由空间光调制器(SLM)生成的 DOPC 波前中直接叠加预设的相位扰动,从而人为引入已知的相位误差并进行研究.
在本节中,我们给出理论分析和实验结果,讨论当 OPC 波前中存在相位误差时,光学相位共轭(OPC)重建信号在穿过散射介质过程中如何发生劣化.
具体情形如下:考虑一个单一光学模入射到随机散射介质上.假设该介质足够厚,使得透射光可以视为由大量互不相关的光学模式组成.如果我们记录这一透射场的相位分布,并在此基础上产生一个相位取相反数的 OPC 场,然后让该 OPC 场再次通过同一散射介质,就可以预期得到强度最优的 OPC 重建信号.
如果我们反而在 OPC 波前中引入随机相位误差,那么可以预期重建的 OPC 信号强度会随之减弱.本节的目的,就是给出这种劣化之间的精确定量关系.
6.1 理论
更为严格地说,上述情形可以用如下数学形式来描述.光在随机散射介质中的传输可用传输矩阵 $t$ 来表征.设单一光学模 $E_a|a\rangle$ 入射到随机散射介质中,其中 $E_a$ 为模 $|a\rangle$ 的复振幅.其透射场可以写成:
$$ \sum_{b} E_a t_{ba} |b\rangle $$
其中 $|b\rangle$表示一个透射出的自由传播模.对应的相位共轭场为:
$$ \sum_{b} E_a^{*} t_{ba}^{*} |b\rangle $$
当该相位共轭波再度通过散射介质时,重建模 $|a\rangle$ 的复振幅变为:
$$ E_a^’ = \sum_{b} E_a^{*} t_{ba}^{*} t_{ab} $$
由于互易性,有 $t_{ab}=t_{ba}$,于是:
$$ E_a’ = E_a^{*} \sum_{b} |t_{ba}|^{2} $$
如果在相位共轭波中存在随机相位误差,则重建模 $|a\rangle$ 的复振幅变为:
$$ E_a’’ = E_a^{*} \sum_{b} |t_{ba}|^{2} \exp(i\phi_b) $$
其中 $\phi_b$ 表示模 $|b\rangle$ 中的随机相位误差.因此,不完美 OPC 信号与理想 OPC 信号的功率之比为:
$$ R_{\mathrm{power}} = \left|\frac{E_a’’}{E_a’}\right|^{2} = \left|\frac{\sum_{b} |t_{ba}|^{2}\exp(i\phi_b)} {\sum_{b} |t_{ba}|^{2}}\right|^{2}. $$
为了计算式(1),我们令每个 $\phi_b$ 取一个在 $-\phi_{\mathrm{range}}/2$ 到 $\phi_{\mathrm{range}}/2$ 之间均匀分布的随机数,并假设 $|t_{ba}|^{2}$ 服从负指数分布,这是因为经过足够厚的随机散射介质后,透射光呈现散斑分布.计算结果如 Fig. 8 中的深色曲线所示.出乎意料的是,该模型预言:随着相位误差增大,OPC 重建信号的衰减其实相对缓慢.即使当 $\phi_{\mathrm{range}} = \pi$(此时相位误差在 $-\pi/2$ 到 $\pi/2$ 之间均匀分布)时,重建的 OPC 信号仍可保留其峰值(无相位误差时)的约 40%.
在上述分析中,入射信号是单一光学模式.利用传输矩阵理论,我们也可以研究入射信号由多个光学模式(即一幅图像)组成的情形.数值计算表明,重建图像随相位误差的变化规律与 Fig. 8 中深色曲线所示的结果相同.
6.2 实验
为了在实验上验证上述理论预言,我们选用了一块散射长度约为 μsl ~ 10 的随机散射介质作为样品.实验步骤与第 5 节所述相同.我们首先利用 DOPC 重建输入信号,并测量重建信号的强度.随后,在生成的相位共轭波中,对每个模式数值叠加随机相位误差,并逐步增大相位误差的取值范围,同时观察 OPC 信号峰值强度的变化.实验结果以蓝色实心方块的形式绘制在 Fig. 8 中,与理论预测符合良好.

Fig. 8: 重建 OPC 信号强度随相位误差大小变化的理论计算结果与实验测量结果对比
6.3 意义
理论和实验结果表明:通过随机散射介质的 OPC 在重建原始光场时,对相位误差具有较强的鲁棒性和容忍度.这说明,在许多基于 OPC 的自适应光学方法中,为了优化实验的其它方面(例如实验速度),在一定范围内牺牲相位精度是可以接受的.举例来说,如果要在 $2\pi$ 范围内精确调制相位分布,就需要大量像素.我们的结果表明,可以采用二值相位调制来获得与精细相位调制相当的 OPC 信号强度,同时显著减少所需像素数量,并提高实验速度.
结论
总之,本文介绍了我们提出的 DOPC 方法这一新型且通用的 OPC 波生成技术的原理、设计和实现过程.与依赖非线性光-物质相互作用的传统 OPC 方法相比,DOPC 既适用于连续波激光,也适用于各种波长和功率的脉冲激光系统.
DOPC 的一个局限在于,其更新速率由波前测量的速度和所用 SLM 的刷新率共同决定.在使用高速商用器件的情况下,整体更新速率有望接近 1 kHz.这个速度虽然仍慢于基于布里渊散射的 OPC 系统,但却明显快于通常采用的 BaTiO₃ 等光折变晶体方法.
DOPC 的一大优势在于,其相位共轭反射率可以任意控制,因为相位共轭波的功率与输入信号的功率无关.这一点是 DOPC 相对于基于非线性光学的 OPC 系统的关键优点.
DOPC 所能处理的自由度数量约为 $10^6$,远高于许多自适应光学系统,与逐像素优化的方法相当,但测量时间却大大缩短.
通过理论分析和实验测试,我们进一步发现,在随机散射介质中,DOPC 对相位误差具有出乎意料的高鲁棒性.这表明,在一定范围内牺牲相位精度,以换取更高的实验速度或更大的自由度容量,是完全合理的.这一结果对许多基于自适应光学的技术具有重要意义.我们预计,DOPC 将在生物医学光学等领域获得广泛应用.